Ein Schritt! Antenne alle Arten von Berechnungsformeln Zusammenfassung
Geschätzte 8 Minuten, um das Lesen zu beenden
Nachdem wir die verschiedenen wichtigen Parameter von Antennen vorgestellt haben, betreten wir einen tieferen Bereich, nämlich die Berechnungsformeln, die sich auf die Parameter beziehen. Jede Formel bringt viel Komfort vor und nach der Installation. Diese Formeln, die in diesem Heft zusammengefasst sind, können nicht nur diverse Fragestellungen beim Einsatz lösen, sondern liefern auch Anregungen für das spätere Antennenlayout .
Der Antennengewinn ist ein Parameter zum Messen des Grades der Direktionalität der Antennenstrahlungsrichtungskarte. Eine Antenne mit hoher Verstärkung gibt einer bestimmten Richtung des Strahlungssignals Priorität. Antennengewinn ist ein passives Phänomen, die Leistung wird durch die Antenne nicht erhöht, sondern einfach umverteilt, um mehr Strahlungsleistung in eine bestimmte Richtung bereitzustellen, als andere isotrope Antennen übertragen.
↓ Im Folgenden finden Sie einige ungefähre Gleichungen für den Antennengewinn.
Allgemeine Antenne
G(dBi) = 10 Lg { 32000 / (2θ3dB,E × 2θ3dB,H)}
In der Formel sind 2θ3dB,E und 2θ3dB,H die Breite der Antennenklappen in den beiden Hauptebenen; 32000 sind die statistischen empirischen Daten.
Parabolantenne
G (dBi) = 10Lg{4,5×(D/λ0)2}
In der Formel ist D der Durchmesser des Paraboloids; λ0 ist die mittlere Arbeitswellenlänge; 4.5 sind die statistischen empirischen Daten.
Aufrechte Rundstrahlantenne
G(dBi) = 10 Lg { 2 L / λ0 }
In der Formel ist L die Länge der Antenne; λ0 ist die mittlere Arbeitswellenlänge.
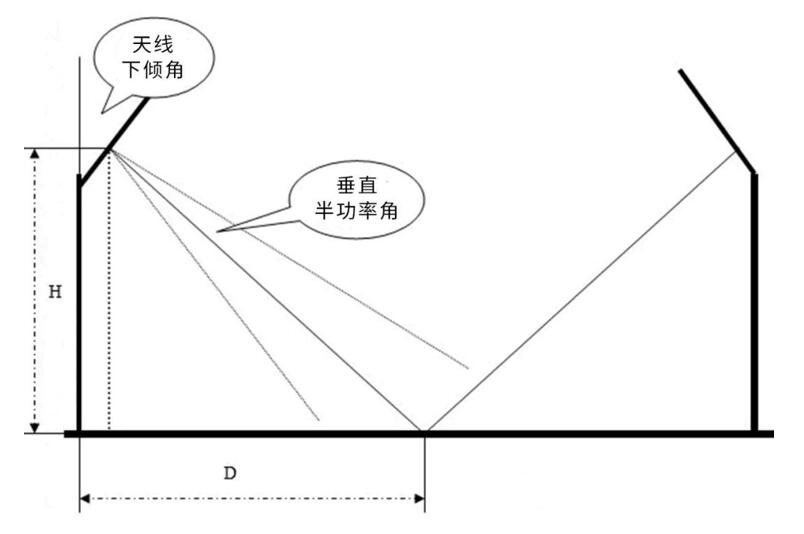
Das Wichtigste bei der Antenneneinstellung ist die Feinabstimmung des Neigungswinkels nach unten (was die Probleme einer schwachen Abdeckung, die sich überlappt, usw. lösen kann). Das Folgende ist eine Einführung in die originellste Methode zur Berechnung des Neigungswinkels der Antenne.
Die Antennenberechnungsformel für stark frequentierte Gebiete (städtisches Gebiet).
Neigungswinkel der Antenne = arctag(H/D) + vertikaler Halbleistungswinkel / 2
Antennenformel für Gebiete mit geringem Netzanschluss (ländliche, vorstädtische Gebiete usw.) .
Neigungswinkel der Antenne = arctag(H/D)
Parameterbeschreibung.
(1) Antennenneigungswinkel: der Winkel zwischen der Antenne und der vertikalen Richtung.
(2) H: Antennenhöhe. Es kann direkt gemessen werden.
(3) D: Zellenabdeckungsradius. Im Allgemeinen wird der D-Wert durch Straßentests bestimmt, um die Abdeckung sicherzustellen, im tatsächlichen Design sollte D im Allgemeinen größer sein, um sicherzustellen, dass sich die Abdeckung zwischen benachbarten Zellen überlappt.
(4) Vertikaler Halbwertswinkel: Der vertikale Halbwertswinkel der Antenne, im Allgemeinen 10 Grad.
Richtungsdiagramm, das Verhältnis des Maximalwerts der vorderen und hinteren Klappe wird als vorderes und hinteres Verhältnis bezeichnet, aufgezeichnet als F / B . Vorher und nachher größer, die Antenne nach der Abstrahlung (bzw. Empfang) kleiner. Vorher und nachher ist das Verhältnis von F / B sehr einfach zu berechnen:
F / B = 10 Lg {(Vorwärtsleistungsdichte) / (Rückwärtsleistungsdichte)}
Parameterbeschreibung: Die F / B-Anforderungen des Antennen-Front-to-Back-Verhältnisses, sein typischer Wert beträgt (18 ~ 30) dB, besondere Umstände erfordern bis zu (35 ~ 40) dB.
Das Verhältnis von Signalspannung und Signalstrom am Eingang der Antenne wird als Eingangsimpedanz der Antenne bezeichnet. Die Eingangsimpedanz hat eine Widerstandskomponente Rin und eine Reaktanzkomponente Xin, das heißt.
Zin = Rin + jXin
Die vorhandene Reaktanzkomponente soll die Antenne von der Speiseleitung bis zur Signalleistungsentnahme reduzieren, daher muss die Reaktanzkomponente möglichst auf Null gestellt werden, dh die Antenneneingangsimpedanz sollte möglichst auf reinen Widerstand gesetzt werden.
Tatsächlich enthält die Eingangsimpedanz immer einen kleinen Reaktanzkomponentenwert, selbst wenn die Antenne gut konstruiert und in Betrieb genommen ist. Eingangsimpedanz und Antennenstruktur, Größe und Wellenlänge, symmetrischer Halbwellenoszillator ist die wichtigste Grundantenne.
Seine Eingangsimpedanz beträgt Zin = 73,1 + j42,5 (Ohm).
Wenn die Länge verkürzt wird (3–5) %, kann die Reaktanzkomponente eliminiert werden, sodass die Eingangsimpedanz der Antenne ein reiner Widerstand ist, dann beträgt die Eingangsimpedanz Zin = 73,1 Ohm (nominal 75 Ohm). Die rein ohmsche Antenneneingangsimpedanz gilt streng genommen nur für die Eckfrequenz. Übrigens beträgt die Eingangsimpedanz des gefalteten Halbwellenoszillators das Vierfache des symmetrischen Halbwellenoszillators, dh Zin = 280 Ohm (nominal 300 Ohm).
Das Verhältnis von Spannung zu Strom an verschiedenen Stellen einer unendlich langen Übertragungsleitung wird als Wellenwiderstand der Übertragungsleitung definiert und mit Z bezeichnet. Die Formel zur Berechnung des Wellenwiderstands eines Koaxialkabels lautet
Z. = [60/√εr] × Log ( D/d ) [Ohm
In der Formel ist D der Innendurchmesser des Kupfernetzes des Außenleiters des Koaxialkabels; d ist der Außendurchmesser der Koaxialkabelseele; εr ist die relative Dielektrizitätskonstante des Isoliermediums zwischen den Leitern. Hinweis: Üblicherweise Z. = 50 Ohm, es gibt auch Z. = 75 Ohm.
Aus obiger Formel ist leicht ersichtlich, dass der Leitungswiderstand nur vom Leiterdurchmesser D und d und der Dielektrizitätszahl εr zwischen den Leitern abhängt, nicht aber von der Leitungslänge, der Betriebsfrequenz und der angeschlossenen Lastimpedanz zum Anschluss der Zuleitung.
Signalübertragung in der Zuleitung, zusätzlich zu den ohmschen Verlusten des Leiters gibt es dielektrische Verluste des Isolationsmaterials. Diese beiden Verluste nehmen mit zunehmender Leitungslänge und Betriebsfrequenz zu. Daher sollte ein vernünftiges Layout so kurz wie möglich sein, um die Länge des Feeders zu verkürzen.
Die Größe der Dämpfung pro Längeneinheit wird durch den Dämpfungskoeffizienten β angegeben, dessen Einheit dB/m (Dezibel/Meter) ist, die auf den technischen Daten des Kabels meist verwendete Einheit dB/100m (Dezibel/Hundert Meter).
Angenommen, die Eingangsleistung des Abzweigs sei P1, die Ausgangsleistung von der Länge des Abzweigs L (m) sei P2, der Übertragungsverlust TL kann wie folgt ausgedrückt werden.
TL = 10 × Lg ( P1 /P2 ) ( dB )
Der Dämpfungskoeffizient ist: β = TL / L ( dB / m )
Im Falle einer Fehlanpassung existieren auf der Speiseleitung sowohl einfallende als auch reflektierte Wellen. An der Stelle, wo einfallende und reflektierte Welle gleichphasig sind, addieren sich die Spannungsamplituden zur maximalen Spannungsamplitude Vmax und bilden ein Wellennetz; während an der Stelle, wo die einfallende und die reflektierte Welle in entgegengesetzter Phase sind, die Spannungsamplituden von der minimalen Spannungsamplitude Vmin subtrahiert werden, wodurch ein Wellenknoten gebildet wird. Die Amplitudenwerte anderer Punkte liegen zwischen Wellenbauch und Wellenknoten. Diese synthetische Welle wird als stehende Welle bezeichnet.
A, das Verhältnis der reflektierten Wellenspannung und der einfallenden Wellenspannungsamplitude, wird als Reflexionskoeffizient bezeichnet und als R bezeichnet.
R = Amplitude der reflektierten Welle / Amplitude der einfallenden Welle = (ZL - Z0) / (ZL + Z0 )
Zweitens wird das Verhältnis der Wellenbauchspannung zur Spannungsamplitude des Wellenabschnitts als Stehwellenkoeffizient bezeichnet, auch bekannt als Stehwellenverhältnis der Spannung, notiert als VSWR : VSWR = Wellenbauchspannungsamplitude.
VSWR = Vmax / Vmin = (1 + R) / (1-R)
Je näher die Anschlusslastimpedanz ZL und die charakteristische Impedanz Z0 liegen, desto kleiner ist der Reflexionskoeffizient R, desto näher liegt das VSWR bei 1 und desto besser ist die Anpassung.


















 5G Netzwerkantenne
5G Netzwerkantenne